MI CUARTO, MI HOGAR
Os presento a Esteban. Su vida es simple. Dormir, jugar y dormir. No trabaja, no estudia. Se tira la mitad del día tumbado en su hamaca, y la otra mitad jugando a las máquinas. Sus padres están cansadísimos de su actitud. No colabora en ninguna tarea de casa.
No tiene apenas amigos porque no sale casi nunca de casa.
Sus padres están preocupados por la actitud de su hijo. Han ideado un plan para que poco a poco Esteban vaya colaborando algo más y sea capaz de relacionarse con otros adolescentes de su edad. Han inventado la RULETA QUITAFLOJERA.
1. LA RULETA QUITAFLOJERA
Esta ruleta es bastante peculiar, pues cada día se hará girar. La flecha apuntará y Esteban esa tarea tendrá que realizar. Podrá gustarle más o menos pero con agrado la hará. Cuando le toque el icono de la siesta, Esteban podrá holgazanear tal y como hace siempre.
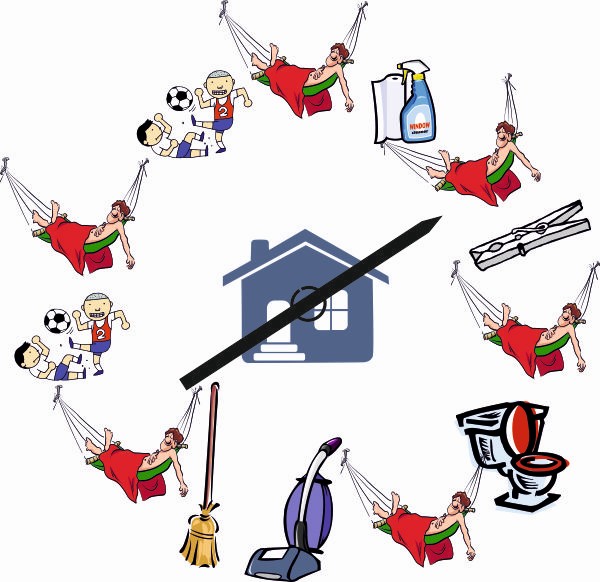
1.1. ¿Cuál es la probabilidad de que Esteban pueda quedarse en su cuarto haciendo lo que le plazca?
1.2. ¿Cuál es la probabilidad de que un día cualquiera le toque tender la ropa? ¿Y salir a hacer deporte?
1.3. De los 30 días que tiene cada mes, ¿cuántos días crees que le tocará pasar la aspiradora? ¿Y de estar a su aire en su cuarto?
2. LUNES: LANZAMIENTOS DE BOLAS CON CERBATANA
Es el primer día en que se pone en juego la ruleta. Tira Esteban y toca “hacer lo que le da la gana”. Primer día y ya no tiene nada que hacer nada, así que dedicará la mañana a uno de sus juegos favoritos: Lanzamiento de papelillos con cerbatana. Consiste en apuntar al cuadrante de coordenadas que hay en la pared, e intentar alinear todos los tiros. Los 4 últimos lanzamientos han dado en los puntos (1,1), (4,2), (0,2/3) y (7,3).
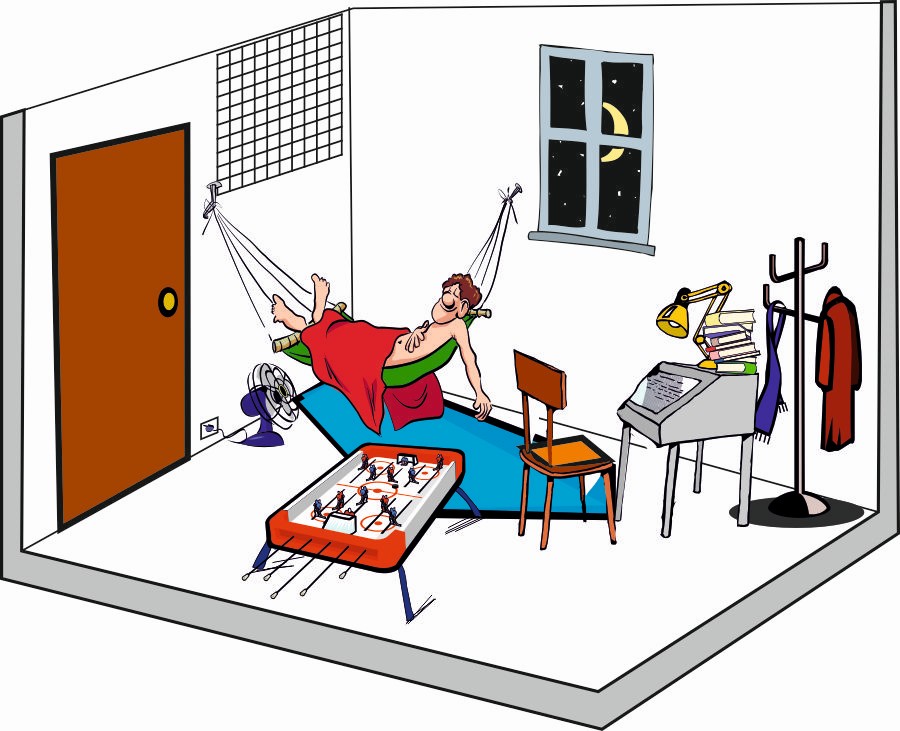
2.1. Dibuja un cuadrante como el que tiene Estaban en su cuarto y coloca en él dónde dieron los 3 últimos lanzamientos. ¿Están alineados?
2.2. Esteban cree que sus tiros están efectivamente alineados. Más aún, cree que todos pertenecen a la recta y=1/3x+1. ¿Cómo se sabe si los 4 tiros están realmente sobre esa recta? Explícalo cuidadosamente. Si no lo estuvieran averigua la fórmula de la recta que los contiene.
2.3. En una ocasión, nuestro muchacho se propuso dar a puntos que estuvieran sobre la recta y=-2x+5. Dibuja otro cuadrante y dibuja esta recta sobre él. Di al menos 5 puntos en los que podía haber dado Esteban.
2.4. El mayor reto afrontado por Esteban en este tan maravilloso entretenimiento, es darle al punto que está sobre las rectas 2x+y=2 e x-y=4 simultáneamente. ¿Podrías decir a qué punto apuntaba el chaval?
3. MARTES: A ORDENAR EL CUARTO
De nuevo se pone en marcha la ruleta. Gira que te gira, la fecha se para en la escoba. Escoba que indica que hay que barrer y ordenar el cuarto de Esteban.
3.1. Esteban decide empezar por ordenar la mesa. Tiene que quitar el polvo de cada uno de los 5 libros y volver a colocarlos sobre la mesa. ¿De cuántas formas diferentes puede hacer el nuevo montón de libros?
4. MIÉRCOLES: LA ARAÑA Y LA MOSCA
Vuelve a girar la ruleta y por fortuna descansar toca el miércoles. Esteban, tumbado en su hamaca piensa qué hacer. Y por sorprendente que parezca no sabe qué hacer. Piensa y piensa, pero su mente solo da vueltas a qué tocará mañana en la ruleta. ¿Y si me tocara pasar la aspiradora? ¿Y si sale hacer deporte? ¡Uff, qué rollo! De repente,…….. sus ojos vieron un araña que caminaba por el techo. Se movía bastante rápido. Esteban siguió con la mirada hacía donde se dirigía y vio una mosca posada al otro lado de la habitación. A por ella iba. La situación es la siguiente:
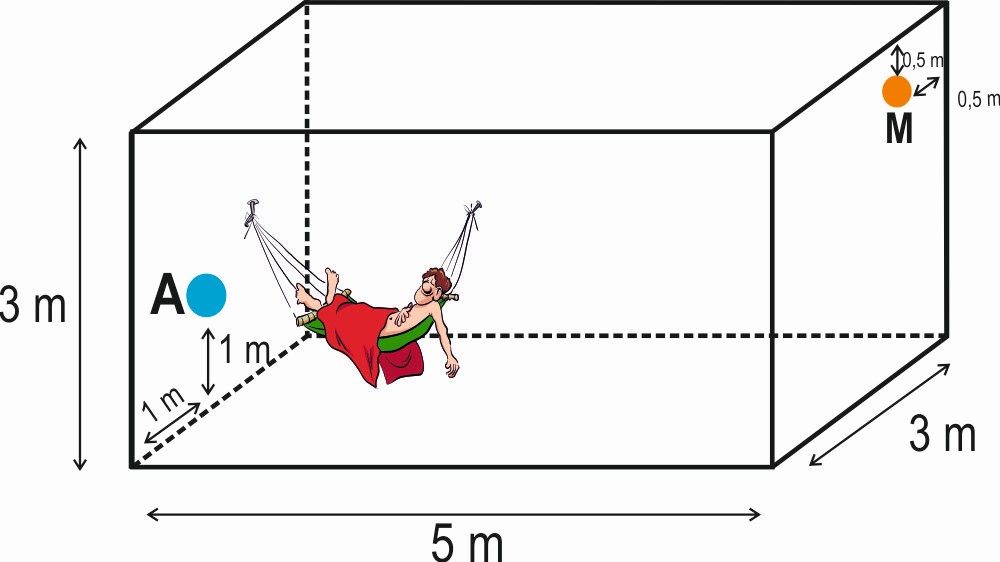
4.1. Esteban ha imaginado qué camino va a seguir la araña. Dibuja la habitación de Esteban (fíjate en el dibujo de arriba y recuerda que este cuerpo geométrico se llama “paralelepípedo”) y sobre ella traza el camino que seguirá la araña para llegar hasta la mosca. Explica por qué has elegido ese camino y no otro.
4.2. Observa el siguiente desarrollo plano de la habitación de Esteban. Señala en él, el camino que elegiste. Haz tus pruebas recortándolo de la hoja final. Procura que al doblar queden los nombres de las paredes hacia dentro de la habitación.
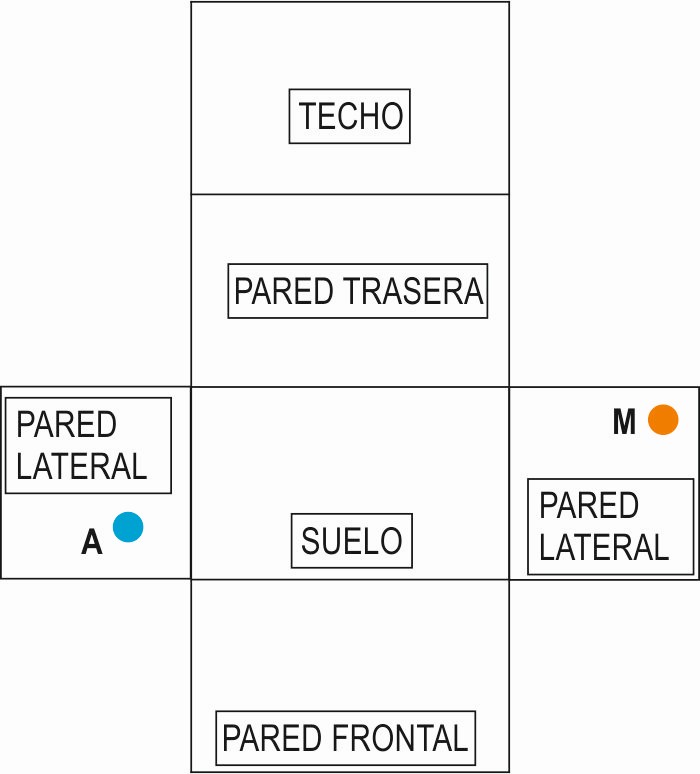
4.3. Usando alguno de los dibujos de los 2 apartados anteriores, calcula la distancia que recorrerá la araña según tu camino elegido.
4.4. Observa otros posibles desarrollos planos de la habitación de Esteban. Coloca en ellos la posición inicial de la araña y de la mosca, y une sus posiciones con una línea recta (si se pudiera). Para que te resulte más fácil, recorta cada modelo y construye la habitación (usa los desarrollos planos grandes que se adjuntan al proyecto).
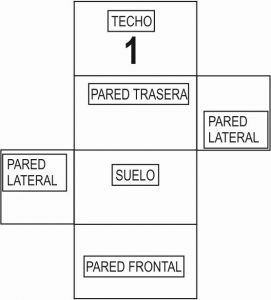
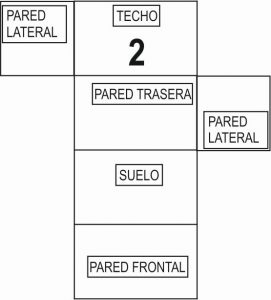
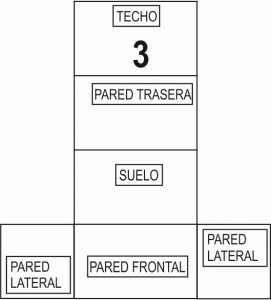
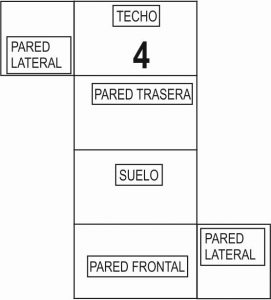
4.5. Dibuja, para cada camino que hayas podido hacer, la habitación de Esteban (en 3D) y marca sobre las paredes dichos caminos.
4.6. Calcula la distancia de cada uno de los caminos del apartado anterior.
4.7. Ya que sabes cómo va esto, busca y encuentra (si puedes) el camino más corto que debe seguir la araña para atrapar a la mosca. Dibújalo.
5. JUEVES: ASPIRADORA
Como era de esperar, una tarea de limpieza le ha tocado a Esteban para este día. Los jueves suele ser cuando Esteban está más perro. ¡Qué esfuerzo más grande tendrá que hacer¡ Cuando se estaba levantado de su hamaca, suena el timbre. Con su ritmo habitual, Esteban se dirige a la puerta y abre. ¡Un vendedor de robots aspirador¡ Enseguida sus ojos se abrieron y despertaron de golpe! ¡Ese señor estaba dispuesto a hacer una prueba de su aparato con fin de poder venderle uno a Esteban!
– Pase usted, buen hombre. Claro que me interesa una prueba. Dice usted que este robot se pone en el suelo y ya solo hay que esperar a que el solito vaya por la casa limpia que te limpia.
– Efectivamente, pero también decirle que su consumo es mínimo, apenas hace ruido y podrá pagarlo en cómodas mensualidades. ¡Todo ventajas!
5.1. Calcula el tiempo (T en minutos) que tardará en aspirar todo el suelo de la habitación de Esteban teniendo en cuenta que el vendedor le ha comentado que dependerá de la superficie (S en metros cuadrados) de la misma según la fórmula:

5.2. Haz una gráfica de dicha relación que relacione esas dos variables descritas en el apartado anterior.
– Señor, ha sido usted muy amable, y su robot es muy chulo. Yo se lo compraría, pero son mis padres los que tienen la última palabra. Venga mañana cuando estén mis padres.
– De acuerdo, mañana volveré a pasarme.
6. VIERNES: PENSANDO EN EL ROBOT
Esteban está de suerte, le ha tocado descanso. Pero algo increíble ha pasado, Esteban no está tumbado en su cuarto, sino que está buscando información de ese fabuloso robot aspirador que probó ayer. Quiere convencer a sus padres para que lo compren. Mira todo lo que ha encontrado en Internet. Ha encontrado en Internet un gráfico sobre cómo ha variado el precio del robot en los meses anteriores.
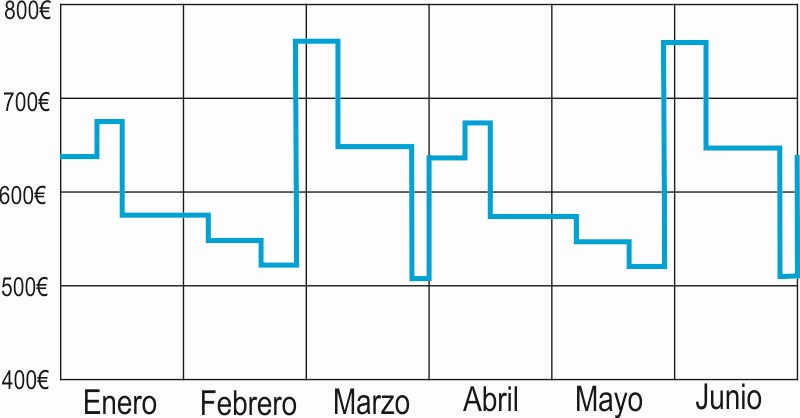
6.1. ¿Entre qué precios se ha vendido este robot en los 6 primeros meses del año?
6.2. Si la evolución del precio de este robot sigue un patrón similar al de la gráfica, ¿cuánto le costará a los padres de Esteban si lo compraran hoy al contado?
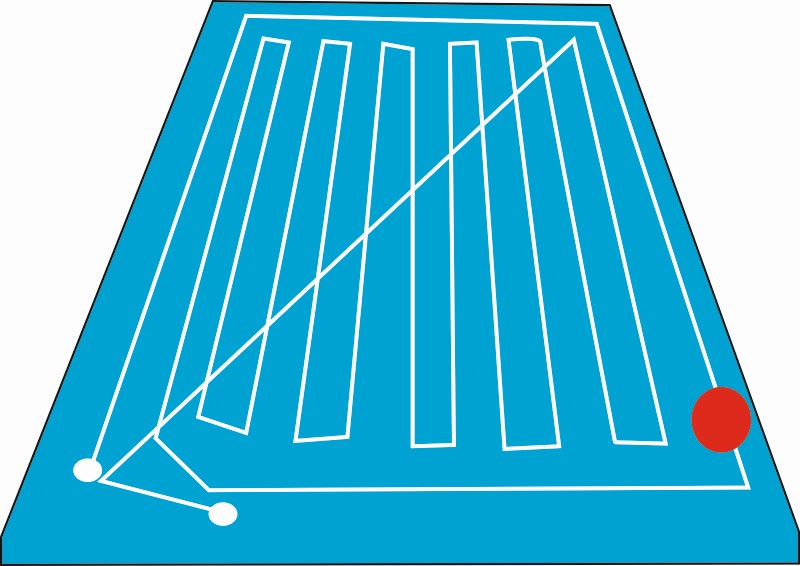
6.3. Durante esa tarde llegó el vendedor y para que terminaran de convencerse les habló del movimiento especial que sigue el robot, que nunca aspira 2 veces el mismo sitio, y que lo podrían pagar en 12 mensualidades, sin entrada, a un interés simple del 5%. ¿A cuánto ascienda cada mensualidad?
6.4. Haz un croquis de la habitación de Esteban y describe el movimiento del robot, sabiendo que es como el de la imagen y que la separación entre las líneas es de 30 cm.
6.5. Con este movimiento, ¿cuánto tardará el robot en limpiar la habitación de Esteban si tarda 5 segundos por cada metro que recorre? ¿Coincide con el resultado de la fórmula de la actividad anterior?
7. SÁBADO: WC
Venga mamá, haz girar la ruleta, que hoy estoy que me salgo. Como toque pasar la aspiradora habré triunfado. Estrenaré mi robot nuevo. Gira que te gira, y……. ¡A limpiar el cuarto de baño! ¡Oh no! ¡Qué mala suerte! Esteban empieza a darle a la cabeza y piensa que quizás existe un robot para limpiar el water. Investiga en Internet y encuentra un curioso estudio realizado a 100 familias sobre la frecuencia en qué limpian el baño y la nota media en matemáticas del curso pasado de su hijo mayor en el colegio e instituto. Esos datos se encuentran en la siguiente tabla:
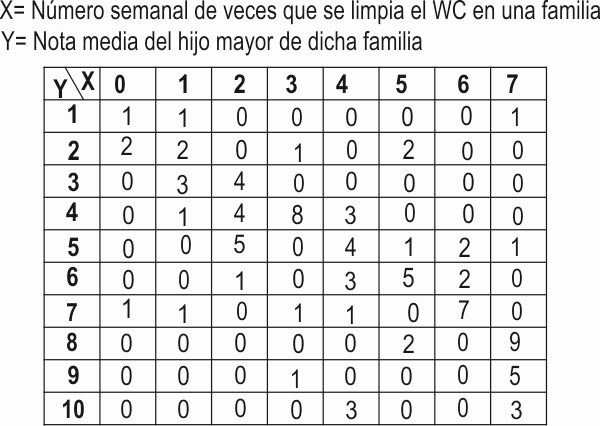
 Esteban observa detenidamente la tabla, y se pregunta:
Esteban observa detenidamente la tabla, y se pregunta:
7.1. Según este estudio, ¿cuántas familias limpian habitualmente el wc más de 3 veces a la semana?
7.2. ¿Cuántas familias tienen hijos que sacan nota media inferior a 5?
7.3. ¿Cuántas familias limpian el WC más de 3 veces y su hijo mayor saca una nota media mayor de 5?
7.4. ¿Hay correlación entre estas 2 variables? ¿Tú qué opinas?
7.5. Viendo los datos, Esteban ha encontrado un fallo de este estudio. ¿Cuál es?
8. DOMINGO: VIENDO PASAR LAS HORAS
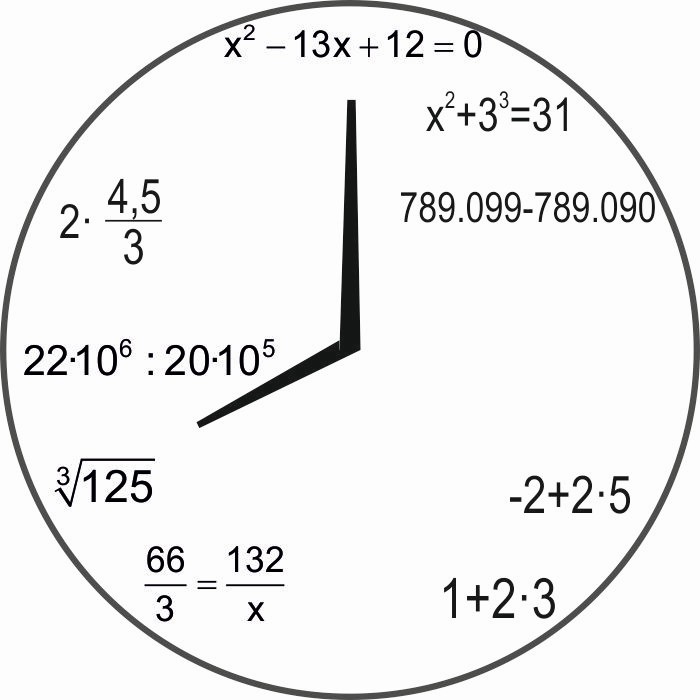
Por fin domingo. No se gira la ruleta. Hasta de eso se descansa. Esteban, ha reflexionado mucho durante esta semana, y ha concluido que el no hacer nada no es bueno ni para la mente ni para el cuerpo. Así que hoy se ha decidido a arreglar su reloj de pared. Hace más de un año se rompió mientras hacía rebotar, una y otra vez, una pelota de tenis contra la pared. En una de esas falló y un buen golpe le dio al reloj. Hasta tal punto que se cayó y todos los números y agujas se dislocaron. Se desmontó por completo.
8.1. Esteban ha reconstruido el reloj, pero no se ha fijado si cada número lo ha colocado en su lugar. Ayúdalo y comprueba si está todo en su sitio.
8.2. Hay varios números que se perdieron. Siguiendo la línea de este reloj, consigue operaciones para los números que faltan.
Descarga la ficha para el alumno en PDF