DE LA TIERRA AL MÁS ALLÁ

Luis: El cohete ya está listo. Ha quedado genial. Nuestro proyecto de Ciencias está preparado. Las medidas del prototipo son las correctas,  80 cm de alto por 36 cm de ancho. ¡Universo, prepárate!

Manuela: ¡El espacio te espere, bonito¡ ¡Lo conseguirás¡   Lo tenemos todo bien estudiado para que llegues muy lejos! 

Ignacio: La cuerda se tensa muy bien.  El impulso será suficiente para colocarte a una buena altura.

1.VERIFICANDO DATOS

Manuela:  Hagamos la simulación del despegue. Luis, coge tus notas y programa el cohete con los valores de la Tierra. Es imprescindible fijarlos bien, pues si no el cohete podría desviarse. Pásame la tabla de los datos.

Luis: Toma.

Manuela: Antes de introducir ningún datos hay que calibrar el sistema.

1.1. Ayuda a calibrar el sistema introduciendo y transformando los valores que se indican a notación científica o a notación decimal.

• Densidad de la Tierra
• Volumen de la Tierra
• Masa de la Tierra
• Distancia que hay entre un punto a nivel del mar situado en el ecuador y el centro de la Tierra.
• Distancia que hay entre un punto situado a nivel del mar en Polo Norte y el centro de la Tierra.
• Superficie terrestre

Ignacio: Calibración terminada.

 

2. DEPÓSITO DE COMBUSTIBLE

Manuela: Ha quedado genial este prototipo. Como las pruebas con él salgan bien, pasaremos al modelo real. ¡Ese sí que es grande,  medirá 12 m de alto y 5,40 m de ancho!

Ignacio: ¿Y cuánto combustible le cabrá en el depósito?

Luis: El depósito del combustible del prototipo tiene forma cilíndrica y mide 2 cm de radio por 5 de alto.
Así que si calculamos un poquito se obtiene una capacidad de aproximadamente ………. 63 cm3 de gasolina.

Luis:  Y por tanto, con un simple cálculo, sabemos que el depósito del cohete real tendrá una capacidad de
aproximadamente 212058   cm3  que equivale  a  unos 212 litros.

Ignacio: ¡Joer! ¿Cómo has sabido todo eso?

Luis: Muy fácil. Para el volumen del prototipo he usado la fórmula del volumen de un cilindro, y para el del cohete
real sólo me ha bastado multiplicar lo obtenido para el propotipo por el cubo de la escala.

2.1. ¿Cuál es la escala con la se ha construido el prototipo?

2.2.  ¿Cómo ha deducido Luis que la capacidad del depósito de combustible del prototipo es de unos  63 cm3 de gasolina?

2.3. ¿Cuál son las dimensiones del depósito de gasolina del cohete real?

2.4.   Calcula el volumen del depósito del cohete real. ¿Cuál es la relación entre los dos volúmenes?

 

3. PROBANDO EL PROTOTIPO

Ignacio: La trayectoria del cohete  no va a ser siempre la misma.  Según tensemos la cuerda, y hacia donde lo dirijamos, la parábola que describirá será diferente. Intentemos mantener siempre la cuerda igual de tensa, y veamos en qué lanzamiento alcanza más altura nuestro cohete.

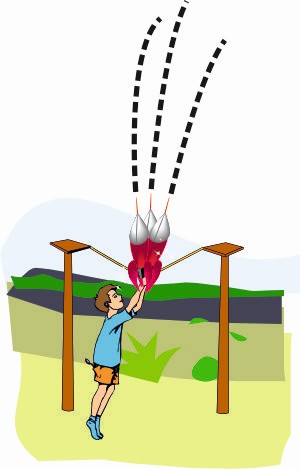
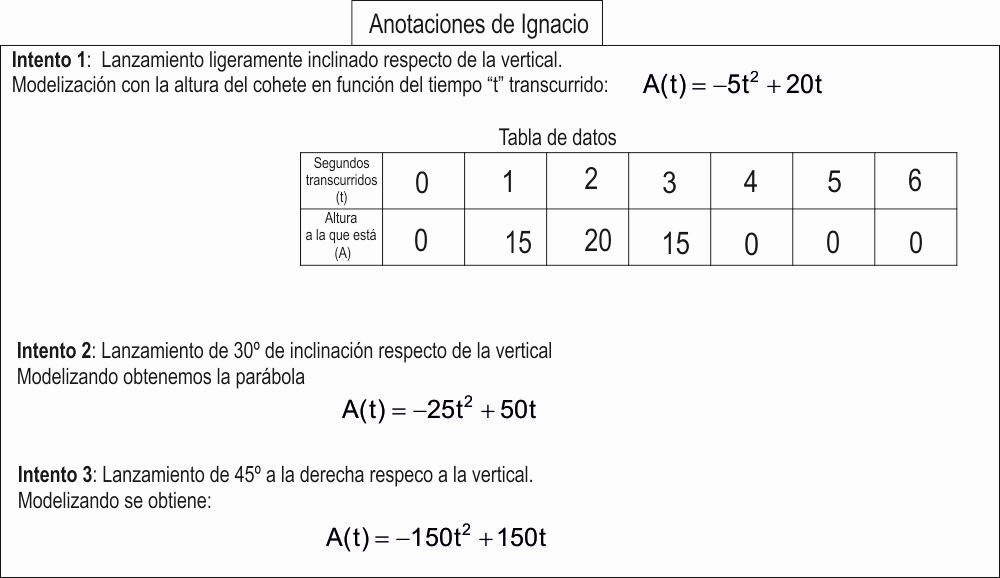
3.1. Viendo la tabla del intento 1, razona cuántos segundos estuvo el cohete en el aire.

3.2. En el instante cero, ¿a qué altura respecto del suelo se encuentra el cohete en cada uno de los intentos?

3.3. Para el intento 2   haz una tabla desde que se inicia el lanzamiento hasta que aterriza en el suelo.

3.4. Haz otra tabla para el intento 3.

3.5. ¿Cuál es la altura más elevada que alcanza el cohete en cada uno de los 3 intentos?

3.6. Aquí tienes las gráficas de los 3 intentos.  Indica a qué intento corresponde cada una de ellas.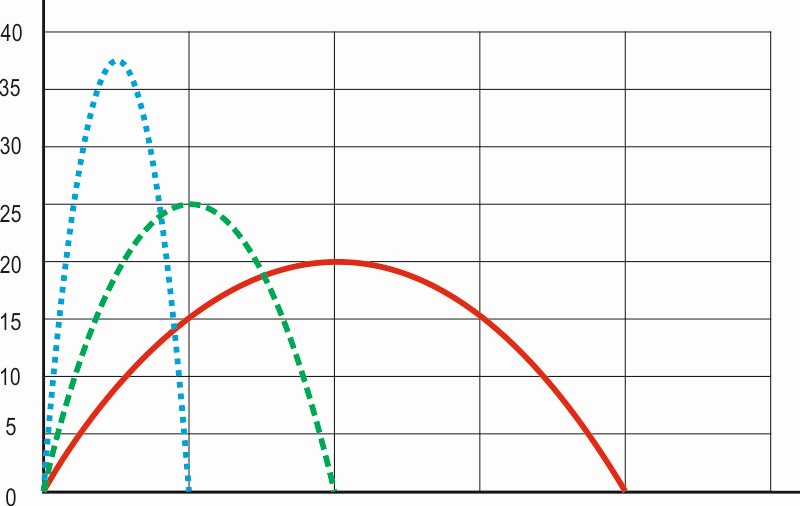

 

4. EN EL HANGAR

Ensamblar todas las piezas del cohete real no es nada fácil. Tienen que hacerlo en el hangar. Lo montarán tumbado y ya cuando esté acabado lo pondrán en vertical. Este es el plano de las instalaciones dónde se fabricará el cohete.

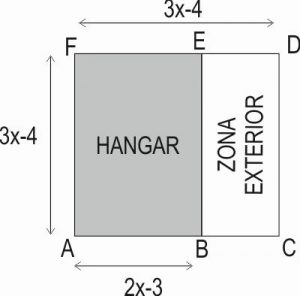
4.1. Explica por qué el valor de x no puede ser 1,3 hm.

4.2. ¿Cuál es el área del hangar expresada en función de x?

4.3. Expresa la distancia ED en función de x.

4.4. Si  x= 1,4 hm , ¿se podrá montar el cohete dentro del hangar?

4.5. Escribe una medida para x, no superior de 2 hm, de forma que sí se pueda montar el cohete dentro.

 

5. LANZAMIENTO FALLIDO

Luis: 3,2,1,….despegue.

Manuela: Despegue efectuado. El cohete sigue la trayectoria prevista.

Ignacio: Espera, ¡algo va mal!

Luis: Hemos perdido contacto. No hay señal.

Manuela: Oh no!  Se han parado los motores.   ¡Camino del fracaso!….

Luis: ¡Nos hemos estrellado!

Ignacio: ¿Dónde?

Manuela: Posición del impacto en:

• Latitud: 37.440970721338765  = 37 º  26 ’ 27 “  Norte
• Longitud: -4.211679267464206 = 4º 12 ’   42 ”   Oeste

5.1. Investiga: ¿Qué son los meridianos y los paralelos? Además de describirlo, incorpora una imagen de la Tierra dónde se vea claramente los meridianos y paralelos.

5.2. ¿Qué es el meridiano de Greenwich?

5.3. ¿Qué es la latitud y la longitud? ¿En qué unidades se mide?

5.4. Explica cómo saber la situación de un punto de la Tierra que tiene Latitud Norte: 45º 12′ y Longitud Este: 34º 15′

5.5. Descubre el lugar exacto dónde ha caído el cohete en la web http://www.coordenadas-gps.com/

 

6. ACABA DE LA MISIÓN

 Manuela: Los sistemas de seguridad han funcionado correctamente. El paracaídas de emergencia ha salvado
al cohete de su completa destrucción.  Los datos de nuestra prueba fallida han sido los siguientes:  

6.1. ¿En qué momento empezaron a fallar los motores al cohete?

6.2. ¿En qué momento exacto se abrió el paracaídas del cohete?

 

7. NUEVOS RETOS: ¿PODRÍAMOS JUGAR AL BILLAR CON LA TIERRA?

Ignacio: Me estaba preguntando, que si el Universo fuera una gran mesa de billar, ¿se podría jugar con la Tierra?

En la realidad las bolas de billar deben ser esferas casi perfectas. Casi perfectas porque se acepta que tengan una desviación máxima de un 0,22%, es decir, que cualquier pequeño bultito o agujero en su superficie no puede medir más de una 0,22% del radio de la bola.   Suponiendo que no hay ninguna montaña en la superficie terrestre y que la única deformación existente en la Tierra es el achatamiento de sus polos, ¿podrías decir si se podría jugar al billar con ella? Será mejor que lo hagas por partes:

7.1. Calcula el 0,22% del radio de la Tierra en el Ecuador.

7.2. Mide cuántos km corresponden al “agujero” que produce el achatamiento de los polos.

7.3. Comprueba si la medida del achatamiento de los polos es inferior o superior a la desviación máxima permitida para jugar al billar.

Descarga la ficha para el alumno en PDF