MATEMÁTICAS DE CINE


1. LA COLA DEL CINE
Acabas de llegar al cine y hay un colón enorme para sacar la entrada. Sólo faltan 15 minutos para que la peli empiece.
Responde a las siguientes preguntas:
1.1. Sabiendo que solo hay una taquilla abierta, ¿cuánto tiempo crees que debes esperar en esta fila si ocupas el puesto 200 en la fila y cada persona tarda 20 segundos en comprar la entrada?
1.2. ¿Te dará tiempo a entrar para verla peli desde el principio?
1.3. Al menos, ¿cuántas taquillas más deben abrir para que puedas ver entera la película?
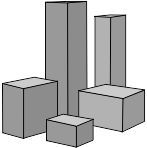
2. ¿QUÉ PALOMITAS ELIJO?
Antes de entrar en la sala para ver la peli, como es tradición ¡hay que comer palomitas! !En este cine las regalan¡
Hay diferentes modelos de paquetes de palomitas. No todos tienen la misma capacidad.
Modelo 1:
 Modelo 2:
Modelo 2:
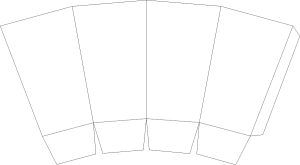
Modelo 3:

Modelo 4:

2.1. Construye los diferentes envases de palomitas. (En la ficha en PDF para el alumno podrás recortarlos a tamaño real)
2.2. Trae palomitas a clase, llena los envases, y enuméralos de menor a mayor capacidad.
2.3. Haz un dibujo de los mismos ya montados y ordenados de menor a mayor capacidad.
2.4. Aunque ya sabrás a qué envase le cabe más cantidad de palomitas, ahora toca averiguarlo matemáticamente. Calcula matemáticamente el volumen que ocupa cada uno de los envases de palomitas que has construido.
Los pasos que tienes que seguir para cada envase son:
- Paso 1. Identificar el cuerpo geométrico que es cada paquete (buscar en internet o en tu libro de mates)
- Paso 2. Tomar las medidas del paquete
- Paso 3. Encontrar la fórmula para calcular la capacidad del paquete (busca en internet o en tu libro de mates).
- Paso 4. Aplicar correctamente la fórmula de volumen correspondiente a dicho cuerpo geométrico.
3. ¿LOCALIZA TU ASIENTO?
3.1. Observa tu entrada. ¿En qué asiento tienes que sentarte? Quizás necesites el desenmascarador de asientos.
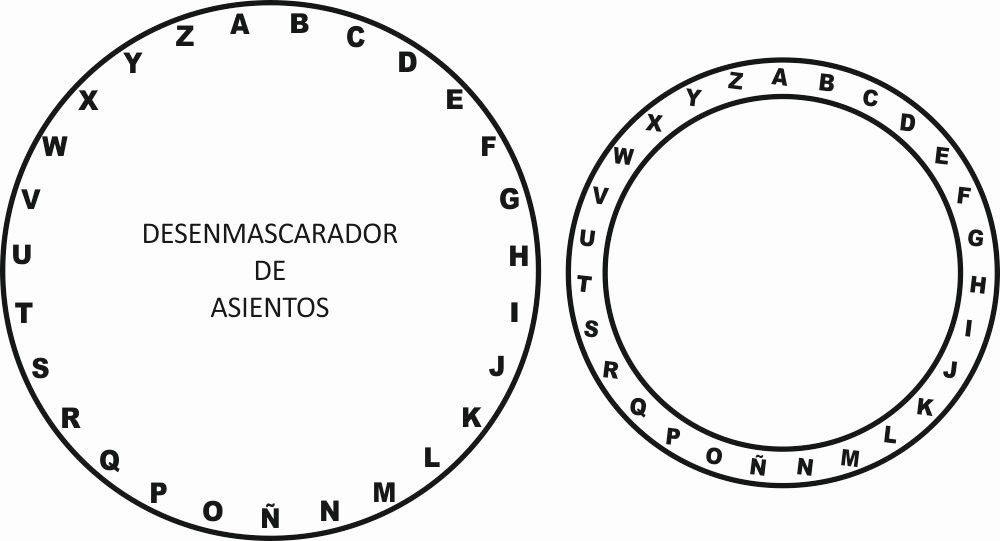

- Paso 1: Transforma cada número el código numérico de tu entrada (mira tu entrada de cine) a su correspondiente letra. ANOTA LA SECUENCIA DE LETRAS QUE OBTIENES.
- Paso 2: Haz coincidir la letra A del círculo pequeño con la letra N del círculo grande.
- Paso 3: Cambia cada letra del asiento que te corresponde por su equivalente en el círculo grande del desenmascador y obtendrás la fila y el asiento que te corresponde.
4. LA SALA 3
Para diseñar una sala de cine, el arquitecto que lo hace, debe tener en cuenta las normativa vigente sobre construcción
de salas de cine. Tiene que velar porque su proyecto cumpla muchísimas cosas. Entre ellas encontramos las siguientes:
- La distancia mínima entre los asientos de una sala de cine es mayor de 1 m.
- Si la pendiente del suelo supera los 20,2º de inclinación, hay que poner escalones.
- Según la norma este ángulo deberá ser de aproximadamente de 30º para el espectador más lejano y como máximo de 80 º para el espectador más cercano.
Responde a las preguntas siguientes
4.1. Este es el dibujo de los asientos del sector central de la sala 3. Complétalo hasta llegar a los asientos más altos (MIRA EL PLANO DE SALA 3).
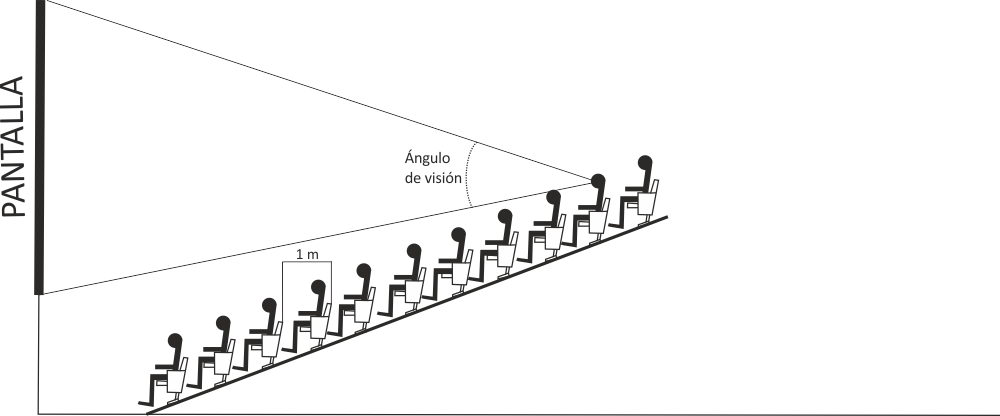
4.2. ¿Qué ángulo de visión tiene un espectador de la primera fila? ¿Y uno de la octava?
4.3. Calcula el ángulo de visión que tendría un espectador de la última fila.
4.4. Según numerosos estudios se ha llegado a la conclusión que el ángulo ideal de visión es de 35º. Si pudieras elegir asiento y sentarte donde se viera mejor, ¿en qué asiento lo harías?
4.5. ¿Qué longitud mínima tiene la sala? Explícalo.
4.6. Al cabo de 1 mes, la sala fue inspeccionada por los arquitectos municipales y concluyeron que tenían que cerrar el cine. Descubre el motivo.
4.7. Pregunta especial: ¿A qué altura aproximada se sitúa el último asiento?
5. EMPIEZA LA PELI
Como casi todos los días le tocó. Se levantó despacio de su silla y cabizbajo se colocó al lado de Don Javier.
– Don Javier: Bueno Gaspar, otra vez tú
– Gaspar: Pues sí, otra vez yo. Don Javier. ¡Es que no se me dan bien las matemáticas!
– Don Javier: ¡Tonterías! ¡A todo el mundo se le dan bien las matemáticas, aunque no lo sepa!
¡Sólo tienes que esforzarte!
Don Javier, el profe de mates, en cada una de sus clases planteaba un nuevo problema de matemáticas.
Y el alumno que más tardaba en resolverlo salía a la pizarra y bailaba un ridículo baile sin sentido.
Todo colorado, Gaspar preguntó al profe:
– Gaspar: ¿Realmente tengo que hacerlo?
– Don Javier: Por supuesto. Son las normas de la clase
Gaspar se preparó, resopló, cogió aire y con la mirada en el suelo empezó a bailar dando unos extraños saltitos, moviendo el tronco con los brazos pegados a la cintura. Todo el mundo se rio.
– Gaspar: ¿Me puedo sentar ya?
– Don Javier: Sí hijo sí. ¡A ver si espabilas!
Gaspar se dirigió a su sitio, pensando la forma de no volver a ser el último ningún día más.
5.1. ¿Cómo continúa la historia? Ahora te toca a ti acabarla. Puede ser todo lo larga que quieras. Intenta no cometer faltas de ortografía y redacta correctamente
6. LOS PROBLEMAS DE DON JAVIER
Resuelve los problemas que el profesor de matemáticas Don Javier, de la peli “El baile del último”(en realidad es «La habitación de Fermat»), puso a sus alumnos.
6.1. Acertijo 1: ¿Qué patrón sigue la siguiente secuencia de números: 5 – 4 – 2 – 9 – 8 – 6 – 7 – 3 – 1?
6.2. Acertijo 2: “Tres cajas de caramelos”
Tenemos tres cajas de caramelos: una tiene caramelos de naranja, otra de limón, y la tercera los contiene mezclados.
Las cajas vienen etiquetadas como «Naranja», «Limón» y «Mezcla», pero se sabe que las tres etiquetas son incorrectas.
La pregunta es: ¿cuántos caramelos será necesario probar para conocer el contenido de cada caja?
6.3. Acertijo 3: “Las tres llaves de luz”
En el sótano hay tres llaves de luz y en el tercer piso están las bombillas que se encienden con cada una de esas llaves. El problema es que no se sabe qué llave corresponde a cada foco y la única manera de averiguarlo sería usando la llave y subir al tercer piso para comprobar. ¿Cuál es el procedimiento para subir la menor cantidad de veces al tercer piso y conocer que llave le corresponde a cada bombilla?
6.4. Acertijo 4: “Las hijas del Profesor Otto”
Un colega le pregunta al Profesor Otto las edades de sus tres hijas y este responde que el producto de sus edades es igual a 36 y que la suma es igual al número del portal de enfrente. El colega mira el portal en cuestión y, tras pensar un momento, dice que le falta un dato. Entonces el profesor Otto asiente y dice: «La mayor toca el piano». ¿Qué edades tienen las tres hijas del Profesor Otto?
6.5. Acertijo 5: ¿Cómo medir exactamente 9 minutos con dos relojes de arena de 4 y 7 minutos?
6.6. Acertijo 6: Recorta las 4 piezas de este puzle:

Tienes que conseguir:
1º. Un triángulo equilátero (recuerda que tienes que usar las 4 piezas). Dibuja la solución
2º Un cuadrado (recuerda que tienes que usar las 4 piezas). Dibuja la solución
Descarga la ficha para el alumno en PDF