MATEMÁTICAS AL RESCATE
Antes de nada nos presentaremos.
Somos el equipo de rescate GRUAL (Grupo de Rescate Universal y Ayuda Local). Nos dedicamos a todo tipo de rescates (personas, animales, desastres naturales) en los medios más diversos (agua, tierra, aire).
Éstos somos nosotros:
Cada año, nuestras intervenciones son más numerosas. El 90% de nuestras intervenciones son debidas a imprudencias. A veces las personas no pensamos bien las consecuencias y la repercusión de nuestros actos. Hacemos las cosas a lo loco sin pensar en el peligro que corremos. En algunas ocasiones, nuestras acciones se pagan caro. En este proyecto pondremos ejemplos de algunos de nuestros rescates, así como de la importancia de las matemáticas en todos ellos. Muchos pensareis que para qué se necesitan las matemáticas, pero cierto es que sin ellas la mayoría de los rescates no se producirían. Cada decisión que tomamos directa o indirectamente se basan en ellas.
1.INCENDIO
Tenemos que estar preparados en todo momento. Como en aquella ocasión en la que nos avisaron que se había producido un incendio en las Sierras Subbéticas. El viento soplaba a 9 km/h y el frente avanzaba con rapidez.
En estos casos, la velocidad del viento es determinante. El viento es el factor más importante en la propagación de un incendio. Se ha modelizado el avance del fuego en función de la velocidad del viento.
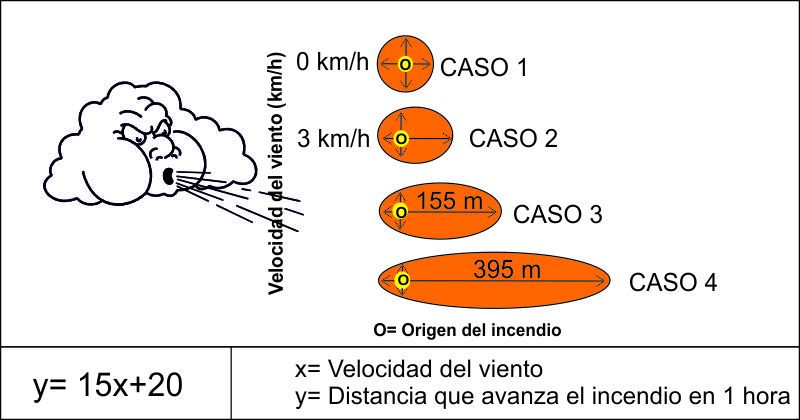
1.1. Transcurrida una hora, ¿qué distancia habrá recorrido el fuego en el Caso 1?
1.2. Según la fórmula, escribe la distancia que avanzará el fuego en el Caso 2
1.3. ¿A qué velocidad sopla el viento en el Caso 3 y 4?
1.4. Si el incendio avanza 260 metros en 4 horas, ¿a qué velocidad soplará el viento?
Esta foto está tomada por un satélite a las 12:00. Es la del incendio en cuestión. Además se han hecho unas anotaciones en él, sobre cómo avanza y dónde se encuentra en este momento.
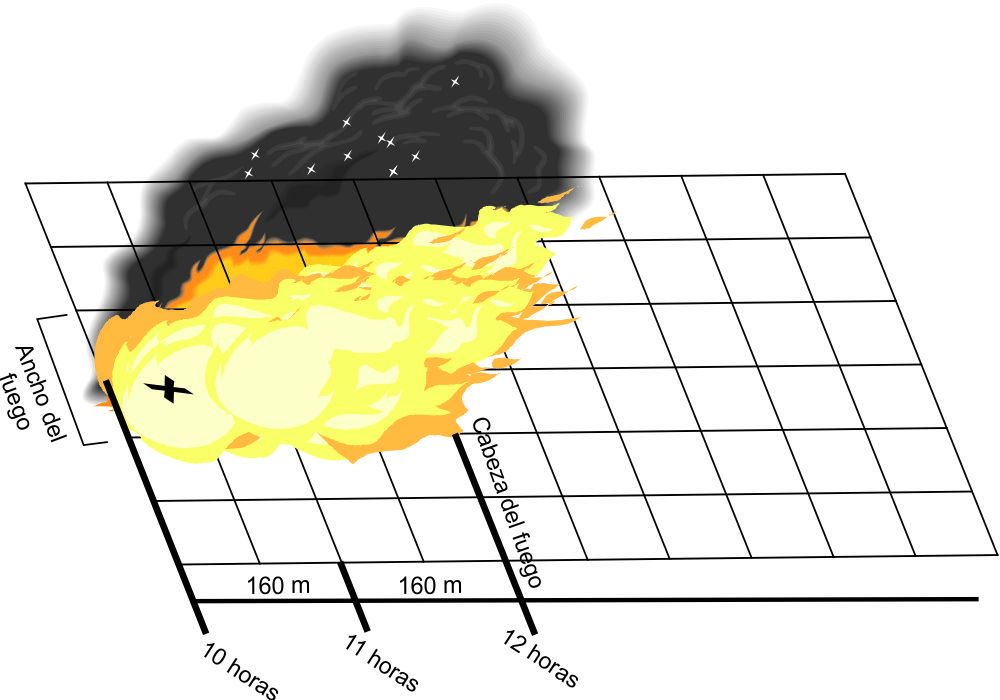
1.5. Los miembros de GRUAL tienen la tarea de realizar un cortafuegos que impida el paso de las llamas. De otras intervenciones, saben que se necesitan 3 horas para que 5 personas puedan hacer un cortafuegos de 200 m de longitud. ¿Cuánto tardarán en esta ocasión para hacer un cortafuegos de esa largura?
1.6. Suponiendo que el fuego avanza al mismo ritmo, ¿cuánto avanzará en ese tiempo?
1.7. ¿Dónde tendrán que hacer el cortafuegos para que durante su construcción nunca se acerque el fuego a ellos a menos de 300 m?
1.8. Cuando el fuego llegue al cortafuegos, éste seguramente podrá ser controlado. Haz una estimación de la superficie total arrasada. Ten en cuenta que el ancho del fuego no varía.
2. CARGANDO AGUA
Para apagar el fuego tenemos la ayuda de nuestro helicóptero.
¿Cuántos litros de agua le caben al compartimento del agua si sus dimensiones son 2x1x1,6 m?
¿Cuántas veces podrá llenar el compartimento si el depósito del que se surte le caben 100000 m3?
3. RESCATE EN LA PLAYA
Es un día ventoso en la playa de La Herradura. Unos bañistas alertan a los socorristas. ¡Otro bañista se ha quedado atrapado con el oleaje! Y aunque no hay muchas olas, el viento en contra impide que pueda salir. Está en una zona que no cubre, a unos 150 m de la orilla. Ante la imposibilidad de que pueda salir por sí mismo, los socorristas de GRUAL acuden al rescate. Piensan que si van directamente a por él, tampoco podrán salir. Además como la lancha de rescate está ocupada en otro servicio, piden colaboración a los usuarios de esa playa para hacer una cadena humana que permita llegar hasta el bañista y rescatarlo.
3.1. ¿Cuántas personas de tu envergadura se necesitarán en la cadena?
4. RESCATE DE MINEROS
Uno de los mayores rescates en los que ha participado nuestro grupo fue el salvamento de 33 mineros que quedaron atrapados en el interior de una mina, tras un derrumbe en la misma. Se les creyó muertos, pero una comunicación milagrosa hizo pensar que algunos aún seguían con vida. La dificultad del rescate fue máxima y duró varios meses. Se ideó un plan de rescate donde primeramente se excavaron varias sondas para llevar alimento a los mineros. Tras ello, se excavó un túnel para rescatarlos. Todo el plan de rescate queda reflejado en el siguiente gráfico:
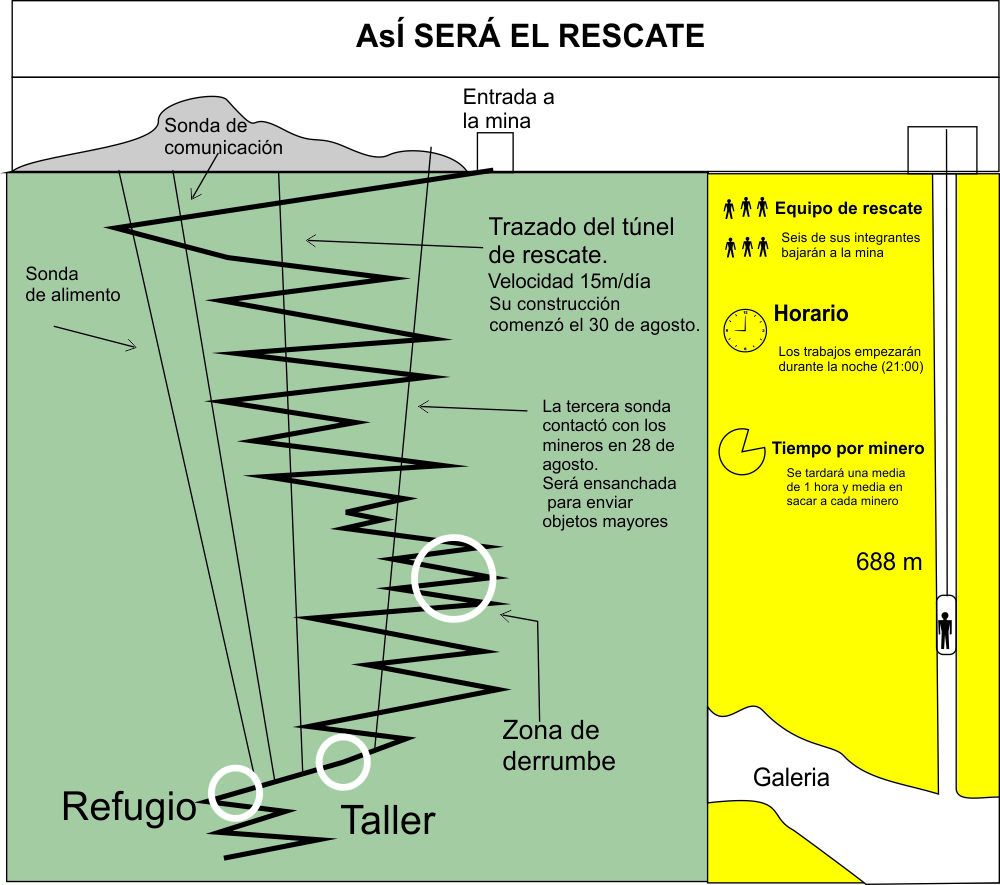
4.1. ¿Cuánto tiempo tardaron en excavar el túnel de rescate? Ten en cuenta que en todo momento hay alguna máquina trabajando.
4.2. Rellena la siguiente tabla que indica el número de días que llevan trabajando en la construcción del túnel y la profundidad que llevan excavada.

4.3. Encuentra una fórmula que relacione las dos variables anteriores.
4.4. Una vez que se terminó el túnel de rescate, ¿cuánto tiempo se tardó en rescatar a todos los mineros?
5. PERDIDO EN LA MONTAÑA
Atención, otro rescate se prepara. Esta vez es un montañero perdido. La familia ha contactado con GRUAL pues el montañero no ha regresado a casa. Salió temprano para hacer una ruta de senderismo de 2 horas.
Han pasado 10 horas y no ha vuelto aún. La familia está muy preocupada. El montañero antes de partir compartió a través de Whatsapp la ruta iba que a hacer con la elevación sobre el nivel del mar de las paradas más significativas por las que iba a pasar. Es la siguiente:
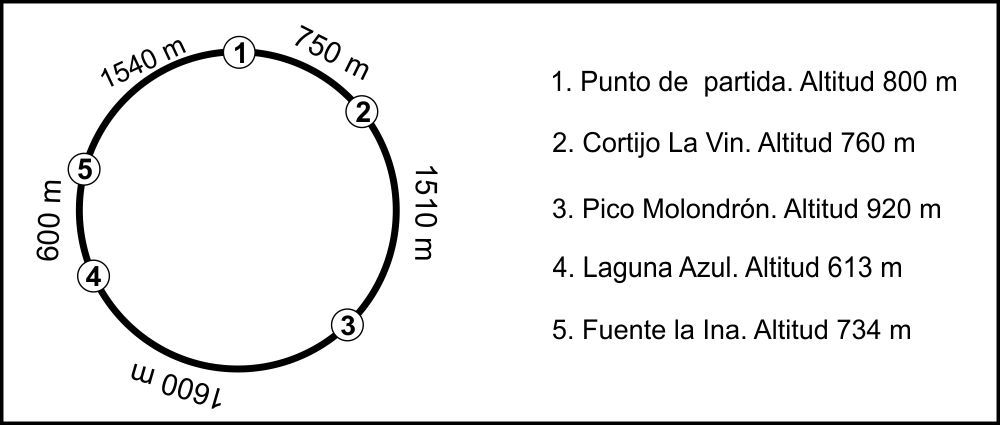
5.1. ¿Cuál es la distancia total de la ruta?
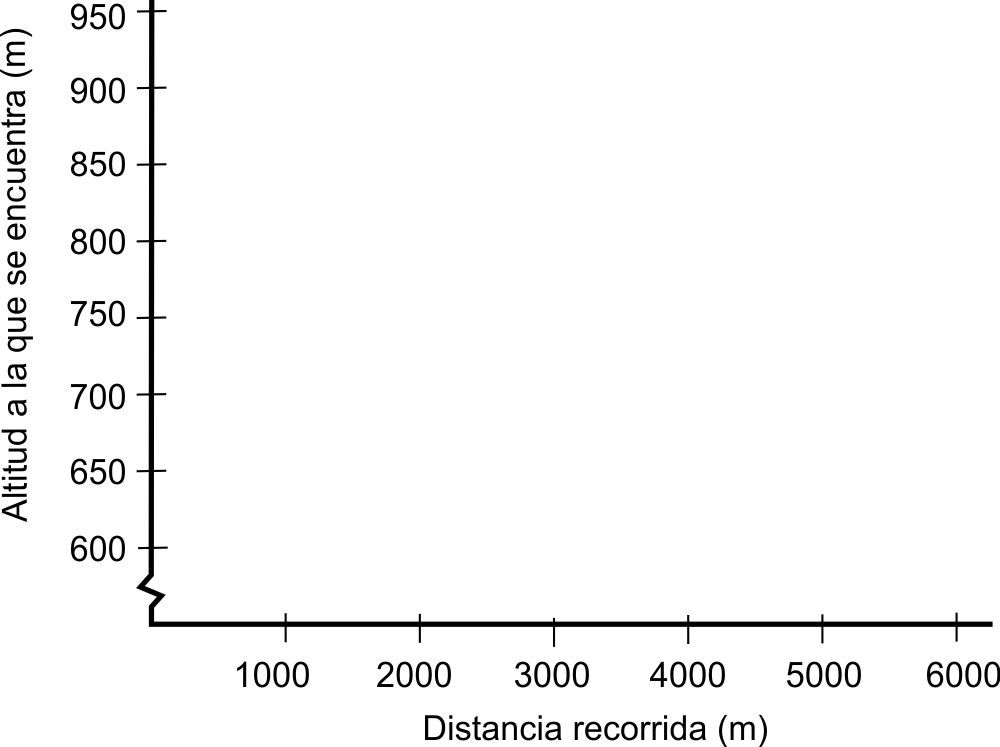
5.2. El equipo de rescate, a la vista de este recorrido y además como
conocedores del terreno, dibujaron un gráfico con el perfil de la ruta. Es
decir, un gráfico que relacionaba la distancia recorrida por el montañero (eje X) y la altitud a la que se encuentra (eje Y). Haz tú también esa
gráfica.
5.3. Otra gráfica que el equipo de rescate GRUAL hizo fue la siguiente:
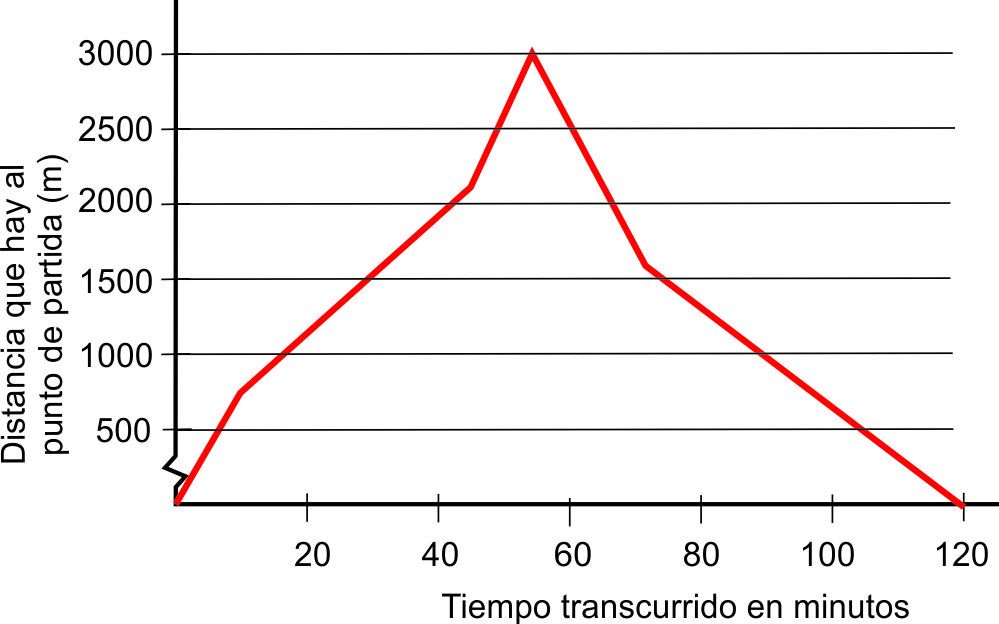
5.3.1. Sitúa sobre la gráfica los diferentes sitios por los que pasó el montañero.
5.3.2. Describe como varía la velocidad en cada uno de los tramos del recorrido.
6. LO QUE CUESTA UN RESCATE DE MONTAÑA
Cientos de senderistas, expertos o turistas aventureros se lanzan cada año a explorar los montes y sierras andaluzas. La escasa preparación, el infortunio o las imprudencias acaban en algunos casos en llamadas de socorro que ponen en marcha un dispositivo de búsqueda y rescate que, además de vehículos y helicópteros, incluye a un gran número de personas que arriesgan su vida para salvar la de otros. Aunque en otras comunidades han puesto un precio a los rescates, en Andalucía todavía no. «La vida de las personas se antepone a cualquier coste económico», asegura un portavoz autonómico. En Andalucía, desde el pasado mes de enero, los servicios de emergencias junto con GRUAL han actuado en 23 sucesos en las sierras de la comunidad, 20 de ellos con helicópteros, con un balance de cuatro fallecidos, 12 heridos, seis perdidos y un desaparecido.
6.1. En total, ¿cuánto habrían tenido que pagar los accidentados o sus familiares si el tiempo medio de cada rescate ha sido de 5 horas, se ha usado 1 coche todoterreno y la cantidad de personas involucradas ha sido de 6 por cada actuación? Guíate por la tabla de tarifas de Cantabria, que sí cobra los rescates.

6.2 En Cantabria, el año pasado, a 31 de agosto, se habían llevado a cabo 154 rescates y este año, a la misma fecha, se realizaron 94. ¿Qué porcentaje ha disminuido?
7. RESCATE DE UN GATO
No todos los rescates son tan peligrosos como los anteriores. En alguna ocasión recibimos llamadas para rescatar mascotas que quedaron atrapadas. Este es el caso de un lindo gatito, que se quedó atrapado en el poyete de la ventana de un granero.

7.1. Sabiendo que la altura total de este edificio es de 12 m, ¿a qué altura se encuentra el gato?
7.2. El grupo de rescate GRUAL siempre lleva consigo una escalera de 3 m de longitud. Para llevar a cabo el rescate con seguridad, la escalera hay que separarla 1 m de la pared. ¿A qué altura apoyará la escalera contra el edificio?
7.3. ¿Será suficiente para llegar hasta el gato?
8. BÚSQUEDA EN EL MAR
GRUAL no solo hace rescates por tierra y aire, sino también por mar. La fragata Fernanda, perteneciente a GRUAL, ha recibido una llamada de S.O.S. cuando está a 50 millas de la costa granadina. Un barco pesquero está en apuros por la fuerte mar que hay en la zona. En el radar de Fernanda, aparece dicho barco.
El radar muestra una serie de círculos concéntricos que indican la distancia a nuestro barco. El círculo más pequeño tiene un radio de 5 millas, el segundo de 10 millas y así sucesivamente. Los diferentes barcos que fondean por la zona aparecen en el radar. Y entre ellos está el pesquero en cuestión.
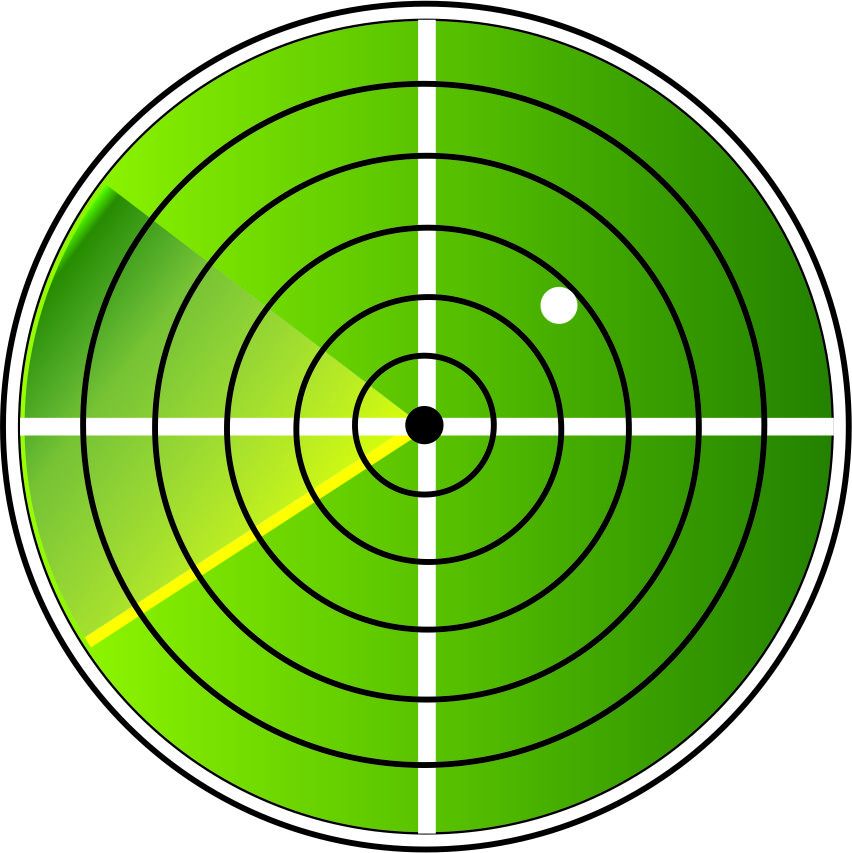
8.1. A cuántos km equivalen una milla? Búscalo en Internet.
8.2. ¿A qué distancia aproximada (en km) se encuentra de nuestra fragata el barco (punto blanco) que aparece en el radar?
8.3. Se ha perdido la señal y no sabemos en qué dirección habrá ido el pesquero. Tras una hora sin comunicación una leve señal avisa que se encuentra en la franja entre las 10 y 15 millas. ¿Cuál es el área (en millas al cuadrado) que ocupa la zona de dicha franja?
Descarga la ficha para el alumno en PDF




