LAS MATEMÁTICAS DEL FÚTBOL

El   Pampalomitos es un modesto equipo cordobés de 2º División.  Sus instalaciones base se encuentran en la localidad de Priego de Córdoba. Su evolución ha sido meteórica, pues tan sólo hace 8 temporadas militaba  en la Tercera División Andaluza.  La clave del éxito, sin duda alguna, es el entrenador, apodado “El  Compae”. El Compae no solo es entrenador, sino que también es profe de matemáticas y aplica sus conocimientos   al fútbol. Aunque eso parece raro, sin duda alguna ha sido la clave del éxito del Pampalomitos.  Lo descubrirás en este proyecto.

1.PRIMER DÍA

El primer día que  El Compae llegó al equipo, se encontró con que la mayoría de los jugadores del equipo eran o habían sido sus alumnos. Algunos de ellos, tal y como les había ocurrido en el instituto, no tenían disciplina alguna. Aunque no era lo único que les faltaba. Tampoco había puntualidad, seriedad, responsabilidad, trabajo en grupo,  autocrítica, etc.  El Compae, no dudó ni un momento. !Quería jugadores que se esforzaran, que fueran capaces de pensar más allá del instante en el que viven.  Por todo ello ideó una serie de medidas que desde el primer momento dieron sus frutos.

En total eran 20 jugadores. Al inicio del primer entrenamiento, El Compae, tras mandarlos callar 3 veces, echó una mirada (y otra, y otra,..) a aquellos que hablaban, y viendo que su actitud continuaba expulsó del equipo directamente, como si de una tarjeta roja se tratara, a la  quinta parte de los jugadores.  Pasó un rato largo hasta que se fueron todos los expulsados.  A los que quedaron les dijo:

– Da igual lo buenos que seáis jugando al fútbol, lo importante es que respetéis a los compañeros, y tengáis modales. Eso, unido a una cierta inteligencia, os hará triunfar. Y como lo que quiero son jugadores inteligentes, os propondré la primera prueba.

Cada jugador tuvo que elegir un dorsal, comprendido entre 1 y 20 (sin repetirse) Aquellos que no fueran capaces de escribir su dorsal usando los números 1,2,3,4, usándolos todos una sola vez, con las operaciones matemáticas de suma, resta, multiplicación y división, serían también expulsados del equipo.

– ¡Y poned paréntesis si los necesitáis! – apuntilló El Compae.

1.1. Después de aquello, la octava parte de los jugadores que quedaban en la plantilla fueron expulsados. De los 20 jugadores iniciales, indica cuántos quedaron en el equipo tras esta prueba.

1.2. Realiza tú la prueba que  puso El Compae a sus jugadores. Aquí tienes un ejemplo.  Hazlo para el resto  de posibles dorsales de los jugadores. Consigue cuántos más números mejor.

2. PRIMERA TEMPORADA

Los inicios son siempre difíciles, y no iba a ser menos para el Pampalomitos.  Apenas si pueden costearse los viajes.  El Compae tiene muy claro que un buen trabajo necesita una buena planificación.  Así que decide dedicar media hora de cada entrenamiento a charlas tácticas. Es más, quiere que sus jugadores aporten ideas. Propone a sus jugadores que construyan  una de esas pizarrillas donde se idean jugadas. De esa forma todos escriben planes y tácticas para  practicarlas  en los entrenamientos y, si son efectivas, también en los partidos oficiales. El Compae hace que todos los jugadores recorran el campo y tomen medidas de sus dimensiones, así como de las zonas básicas del mismo. Las necesitarán para hacer su pizarrilla.

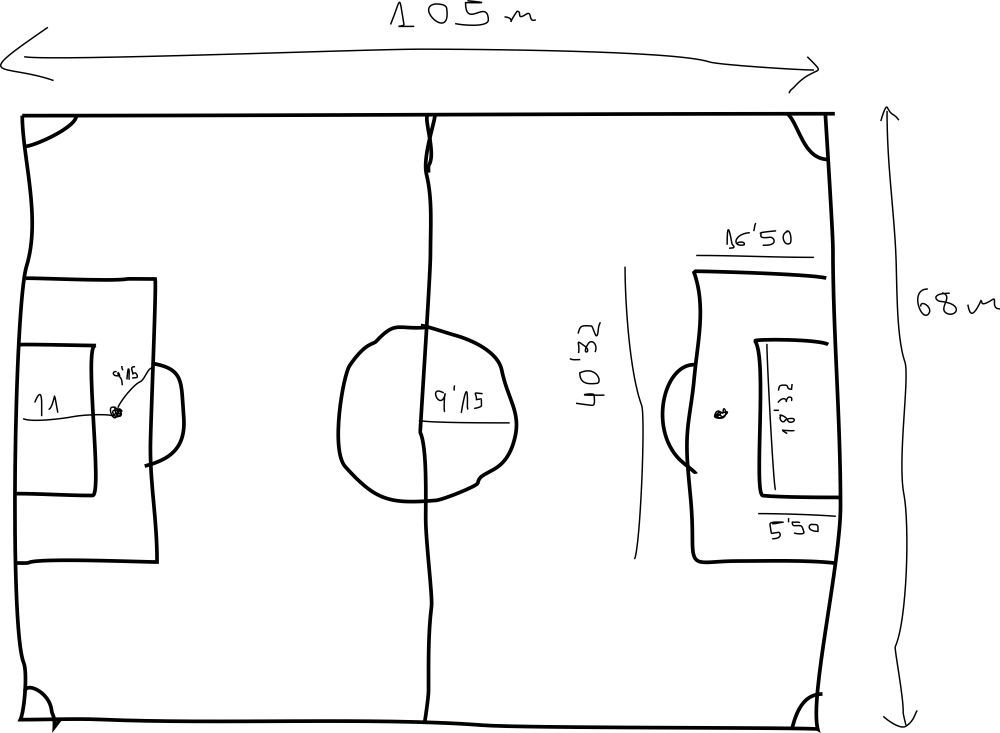
2.1. Realiza tú un plano (tú pizarrilla) a escala 1: 500 del campo de fútbol del Pampalomitos. Ayúdate de las medidas que tomó uno de los jugadores:

3. PLANTAR CÉSPED

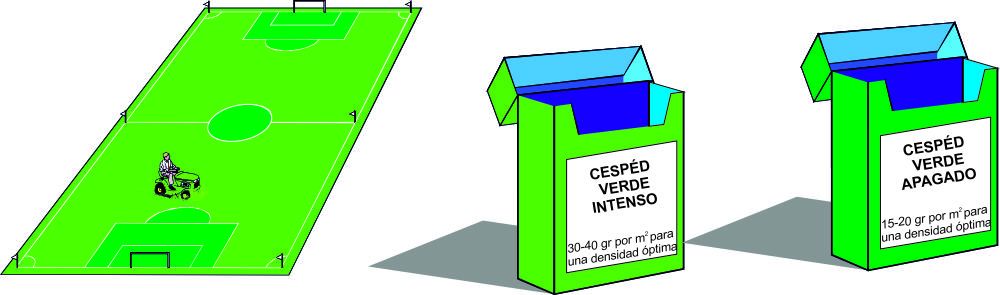
Otra cosa necesaria es plantar césped en el  campo, pues éste es de tierra. ¡Los jugadores están hartos de  rasparse cada vez que se caen! Van a plantar 2 tipos de césped,  verde intenso  para las áreas y  centro del campo, y verde apagado  para el resto de partes del campo incluido el perímetro exterior de todo el campo que tiene 1 metro de anchura.

3.1. Calcula cuánto césped de cada tipo tienen que preparar.  Mira la caja de cada tipo de  semillas de césped.

3.2. Una vez plantado el césped, hay que pintar las líneas blancas del campo. Sabiendo que se necesita 1 litro para cada medio metro cuadrado. y que el grosor de las líneas es de 12 cm, ¿cuántos litros de pintura  se necesitarán para pintar todas las líneas?

4. SEGUNDA TEMPORADA

El Pampalomitos  ha conseguido ascender de categoría. La temporada que viene militará en Segunda División Andaluza, junto a otros equipos de la comunidad.

Esta categoría la disputan 8 equipos de toda Andalucía, uno por cada provincia.  Son los siguientes:

• C.F. Gibraleón (Gibraleón, Huelva)
• Atlético Casariche (Casariche, Sevilla)
• El Rincón (Rincón de la Victoria, Málaga)
• Rácing de Úbeda  (Úbeda,Jaén)
• C.D. Huétor Tájar (Huétor Tájar, Granada)
• Real Adra (Adra, Almería)
• Jerezano (Jerez, Cádiz)
• Pampalomitos (Priego de Córdoba, Córdoba)

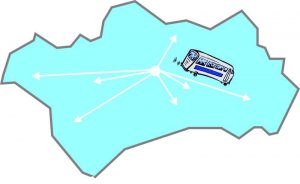
4.1. La empresa de autobús que contrata el club, cobra, lógicamente, en función de la distancia que recorre, a razón de 100€ fijos por desplazamiento y de 0,5€ por cada km recorrido.

– Elabora una tabla con el coste a cada destino.

– ¿Cuál es el coste total del transporte durante toda la temporada?

– Encuentra una fórmula matemática que permita obtener el coste del autobús (C, en €) para cierta distancia   D (en Km).

4.2. Eso de ascender de categoría es bastante  costoso.  El club anda escaso de fondos, y económicamente va a ser una temporada difícil. El Compae, junto con los jugadores, están buscando la forma de conseguir dinero para financiarse los viajes, el material, el coste del arbitraje, etc.

A Tonino, se la ha ocurrido hacer una rifa.  Normalmente las rifas funcionan bien y se suele sacar bastante dinerillo. Van a sortear una camiseta firmada por todos los jugadores. ¡Quién sabe si en el futuro el Pampalomitos será un grande del fútbol español! ¡Entonces sí que se revalorizará la camiseta!

¿Cuántas papeletas han de vender  para poder financiarse los desplazamientos?

¿Si comprarás una papeleta, ¿Cuál es la probabilidad de que te toque la camiseta?

5. FIN DE LA SEGUNDA TEMPORADA

Tras finalizar la temporada, los resultados de todos los partidos fueron:

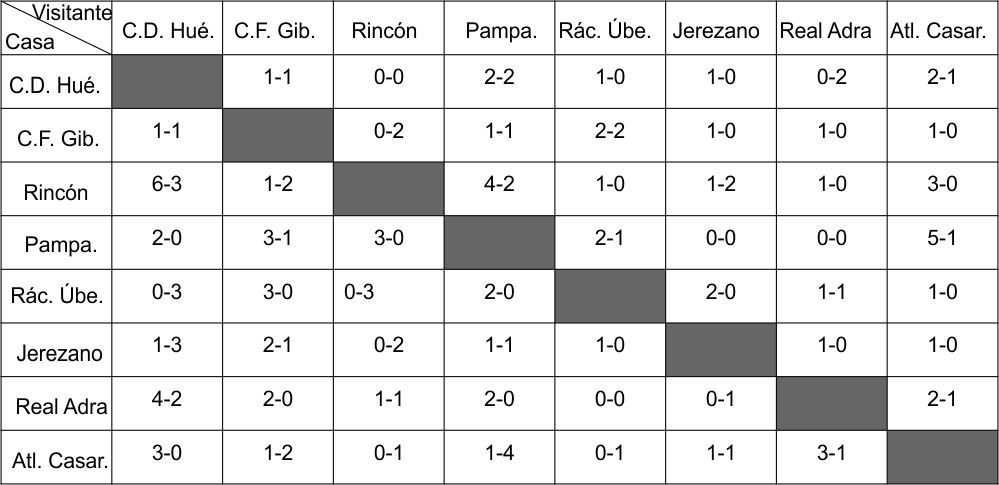
Elabora la tabla clasificatoria de los 8 equipos de la liga. Las columnas que debe contener son:

PJ= Partidos Jugados

PE= Partidos Empatados

PG=Partidos Ganados

PP=Partidos Perdidos

GF= Goles a Favor

GC= Goles en Contra

PUNTOS = Puntos totales obtenidos. Se obtienen así:

Partido Ganado = 3 puntos

Partido Empatado = 1 punto

Partido Perdido = 0 puntos

6. LOS JUGADORES

Al finalizar la liga, los números de cada jugador han sido:

6.1. Inventa una fórmula para decidir cuál de todos los jugadores ha sido el de mejor rendimiento del  equipo. ¿Qué datos utilizas para ello?

6.2. Según tu fórmula, elabora una tabla con los 10 mejores jugadores del equipo.

7. LAS ARMAS DEL EQUIPO: LANZAMIENTO DE PENALTIS

Miguel Povedano es un consumado lanzador de penaltis.  Sus números son increíbles.  De los 11 penaltis que lleva lanzados en las dos temporadas que lleva en el equipo, no ha fallado aún ninguno. Él, siempre ajusta la pelota lo máximo posible al poste derecho o izquierdo, por bajo o por alto. Ajusta tanto y chuta tan fuerte, que por mucho que se estire el portero, no llega. ¿Seguirá con esa efectividad?

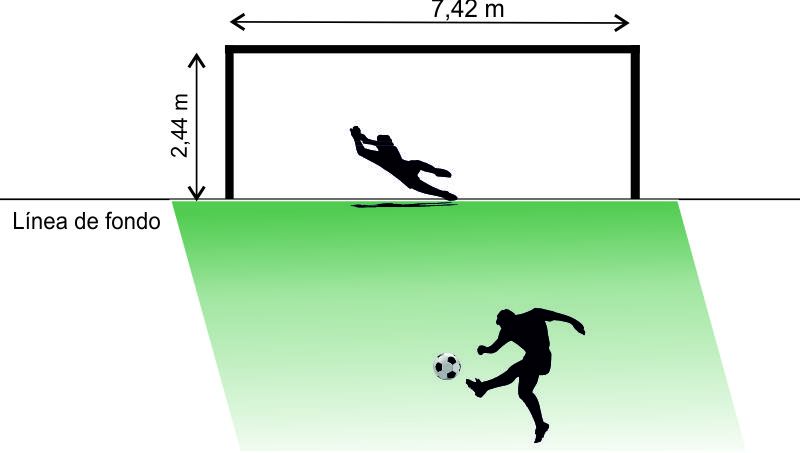
Decide si marcará el penalti en las siguientes situaciones:

7.1. Penalti 1: La pelota se sitúa en el punto de penalti (a 11 m) de la portería, que mide 7,42 m entre poste y poste. El jugador lanza la pelota a ras del suelo, recorriendo una distancia de 11,75m antes de rebasar la línea de fondo.  ¿Será gol?

7.2. Penalti 2: La pelota se sitúa en el punto fatídico a 11 m de la portería. El jugador lanza la pelota a ras del suelo 18º hacia la derecha de la línea imaginaria que une el punto de penalti con el centro de la portería. El guardameta, engañado, se tira hacia el otro lado. ¿Será gol?

7.3. Penalti 3: Esta vez el jugador lanza directo a la escuadra. El portero, que tiene con los brazos estirados  una envergadura de 2,60 m, ¿cuánto debería saltar para que, en el caso de acertar la dirección del lanzamiento, desviar la pelota?

8. LAS ARMAS DEL EQUIPO: ÁNGULOS DE TIRO

El Compae siempre insiste en lanzamientos que tengan un buen ángulo de tiro.  Tras varios días escuchando al entrenador, Frederic se atrevió a preguntar:

Eso del ángulo de tiro, ¿qué es?

Al instante varios jugadores levantaron la mano y afirmaron que ellos tampoco lo sabían.

– ¡¡Si no sabéis matemáticas, para que os metéis a futbolistas!! – exclamó El Compae.

– Os lo explicaré.-  Cogió su pizarra y empezó a dibujar:

8.1. ¿Cuál es ángulo de tiro de este jugador? ¿Cómo y cuánto mide ese ángulo?

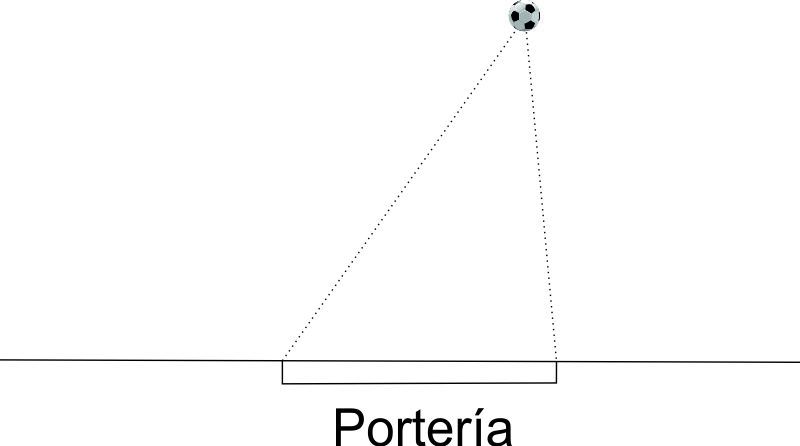
8.2. ¿Cuál de estos jugadores tiene mayor ángulo de tiro? ¿Cuánto mide cada uno?

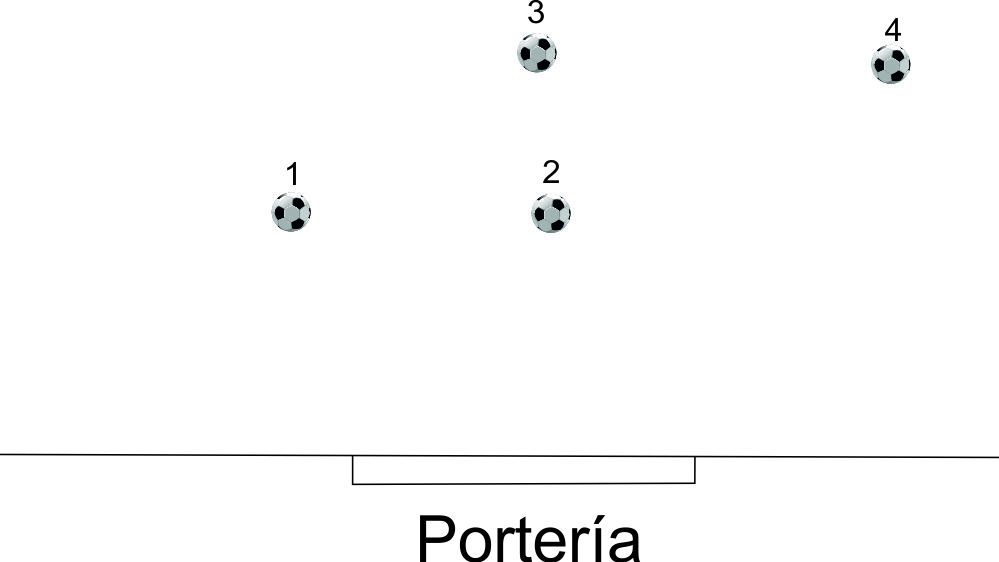
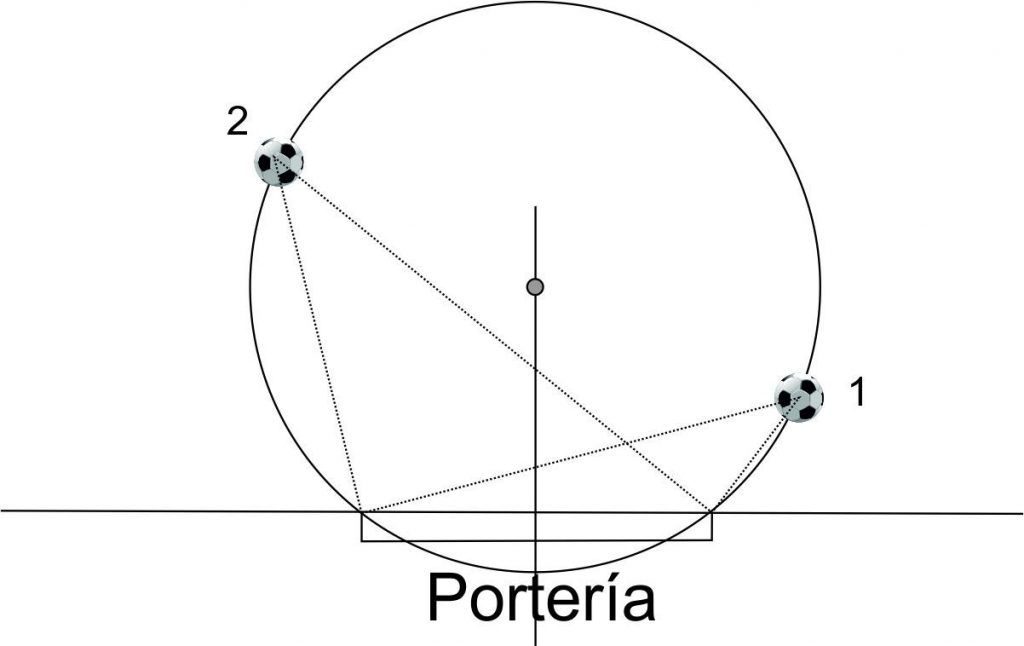
Cuando El Compae les dijo que dibujaran 3 jugadores que tuvieran exactamente el mismo ángulo de tiro, todos se quedaron pillados. ¡Nadie supo colocar a los jugadores en el sitio adecuado! Así que les dio las siguientes instrucciones para hacerlo:

1) Dibuja el segmento que une los postes de la portería.

2) Dibuja la mediatriz de dicho segmento. Recuerda que la mediatriz de un segmento es la recta perpendicular a dicho segmento que pasa por el centro de éste.

3) Elige un punto de esa mediatriz y traza la circunferencia que pasa por los postes y tenga como centro ese punto.

4) Todos los puntos de dicha circunferencia tienen el mismo ángulo de tiro (también conocido como      ángulo inscrito de la circunferencia). De hecho el ángulo de tiro es la mitad del arco de circunferencia  que cortan sus lados.

8.3. Siguiendo estas instrucciones dibuja 3 jugadores con el mismo ángulo de tiro.

8.4. Mister, levantó la mano Frasco. Yo he hecho lo que ha dicho, pero hay algo que no entiendo.  Si estos 3 jugadores que he dibujado tienen el mismo ángulo de tiro, ¿no debería ser igual de fácil marcar un gol desde cualquiera de esas 3 posiciones? Pero en cambio, en la realidad, no es así.

Explica porque es más difícil marcar un gol desde la posición 1 que desde la posición 2.

9. TROFEO PUÑOS DE ORO

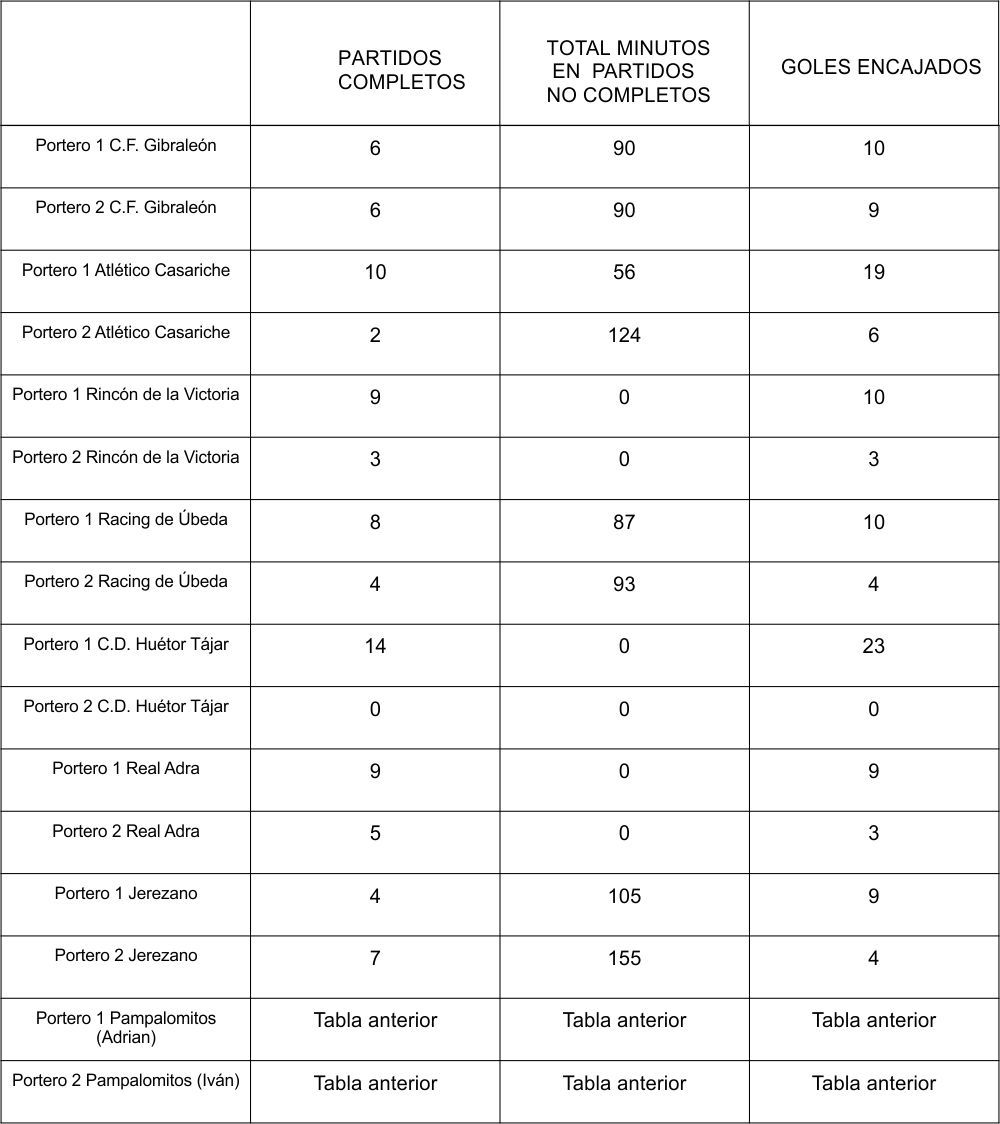
Los porteros de esta liga compiten por llevarse el trofeo Puños de Oro.  La puntuación la obtienen aplicando la fórmula siguiente a aquellos porteros que han jugado tantos minutos como el equivalente a 5 partidos.  El ganador es el que tenga la puntuación más alta.

9.1. Con los datos de la tabla siguiente, calcula la puntuación de cada portero y decide quién se lleva dicho trofeo.

Descarga la ficha para el alumno en PDF